信号去噪之小波变换

发表于 更新于 阅读次数： 本文字数： 1.9k 阅读时长 ≈ 7 分钟

在前面的文章 信号去噪 中简单介绍了常见的去噪方法，以均值滤波和中值滤波做了示例，今天再继续介绍小波变换。

小波变换

小波变换（Wavelet Transform）是一种信号处理和数据分析技术，用于在时间和频率上分析信号的不同特征。与傅立叶变换不同，小波变换具有多尺度分析的能力，允许在不同的时间尺度上检测信号中的特征。

1. 基本概念

信号分解与重构

小波变换的核心思想是将一个信号分解成不同尺度和频率的小波成分，然后可以根据需要重构原始信号。这种分解和重构过程涉及到两个主要函数：小波函数（wavelet）和尺度函数（scaling function）。

  • 小波函数通常表示为 ψ(t)，它是一个用于分析信号的基本波形。不同的小波函数对信号的不同特征有不同的敏感度。

  • 尺度函数通常表示为 φ(t)，它是一个用于描述信号在不同尺度上的版本的函数。通过对尺度函数进行缩放和平移，可以生成不同尺度的小波函数。

2. 连续小波变换（Continuous Wavelet Transform, CWT）

连续小波变换将信号与一组连续尺度和平移的小波函数进行卷积，以获得信号在不同尺度和位置上的表示。这产生了一种时频分析，其中你可以看到信号在时间和频率上的变化。连续小波变换的数学表达式如下：

$$
CWT(a, b) = \int_{-\infty}^{\infty} x(t) \cdot \frac{1}{\sqrt{a}} \psi^*\left(\frac{t - b}{a}\right) dt
$$

其中，$x(t)$ 是原始信号，$\psi(t)$ 是小波函数，$a$ 和 $b$ 分别是尺度因子和平移因子。

3. 离散小波变换（Discrete Wavelet Transform, DWT）

连续小波变换的主要缺点是计算量大，不适用于数字信号处理。因此，离散小波变换应运而生。离散小波变换将信号分解成一系列离散尺度上的小波系数。它是一种多尺度分析方法，适用于数字信号处理和图像处理。

离散小波变换的基本思想是通过一系列滤波器来对信号进行分解。这些滤波器包括高通和低通滤波器，用于提取信号中的高频和低频成分。通过不断迭代分解过程，可以得到不同尺度的小波系数，其中高频系数表示信号的细节，而低频系数表示信号的趋势。

4. 小波包变换（Wavelet Packet Transform）

小波包变换是离散小波变换的扩展，它提供了更大的灵活性和分析能力。与离散小波变换不同，小波包变换允许你对信号进行更细致的分解，以获得更多尺度上的信息。

5. 小波变换的应用

小波变换在信号处理和数据分析中有广泛的应用，包括：

  • 信号去噪：小波变换可以有效地去除信号中的噪声，同时保留信号的关键特征。

  • 时频分析：小波变换允许你在时间和频率上同时分析信号的特征，因此在音频处理和图像处理中特别有用。

  • 压缩：小波变换可以用于信号和图像的压缩，例如JPEG2000图像压缩算法。

  • 特征提取：小波变换可以用于从信号中提取特定的特征，如边缘检测、频率成分分析等。

信号去噪中的应用

小波变换在信号去噪中的应用是其重要的应用之一。它能够有效地去除信号中的噪声，同时保留信号的有用信息。以下是在信号去噪中应用小波变换的一般步骤：

  1. 采集信号：首先，你需要采集包含噪声的原始信号。这可以是来自传感器、仪器或其他数据源的信号。

  2. 小波分解：使用小波变换将原始信号分解为不同尺度上的小波系数。分解通常包括多层级的小波变换，每一级都会产生一组高频和低频系数。

  3. 噪声识别：在分解的小波系数中，噪声通常表现为高频成分或低频成分的异常值。你需要确定哪些小波系数包含噪声，并且需要选择适当的阈值来识别它们。

  4. 阈值处理：将噪声系数置为零或减小它们的幅度，以便去除噪声。这个步骤通常涉及到一个软阈值或硬阈值的函数。

    • 硬阈值：如果小波系数的幅度小于阈值，将其设置为零。

    • 软阈值：如果小波系数的幅度小于阈值，将其减小到零，并且减少的幅度取决于阈值和小波系数的幅度之间的差距。

  5. 小波重构：使用处理后的小波系数，通过逆小波变换重构信号。这将生成一个去噪后的信号，其中噪声成分已被移除。

  6. 性能评估：评估去噪后的信号与原始信号之间的差异。这可以使用信噪比（SNR）等指标来完成。

示例

在 Python 中，你可以使用多个库来执行小波变换，包括 PyWavelets 和 SciPy。这些库提供了丰富的小波分析工具和函数，可用于不同类型的信号处理任务。

以下是 Python 中使用 PyWavelets 库进行信号去噪的示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import pywt
import numpy as np

# 1. 采集信号（假设为含噪声的信号）
signal = ...  # 你的信号数据

# 2. 小波分解
coeffs = pywt.wavedec(signal, 'db4', level=3)  # 使用 'db4' 小波基函数，分解到3级

# 3. 噪声识别

# 4. 阈值处理（假设使用软阈值）
threshold = 0.1  # 阈值的选择取决于你的数据和噪声性质

def soft_threshold(x, threshold):
    return np.sign(x) * np.maximum(np.abs(x) - threshold, 0)

denoised_coeffs = [soft_threshold(coeff, threshold) if i > 0 else coeff for i, coeff in enumerate(coeffs)]

# 5. 小波重构
denoised_signal = pywt.waverec(denoised_coeffs, 'db4')

# 6. 性能评估
# 可以计算信噪比等指标来评估去噪效果

这只是一个基本示例，实际中的信号处理和噪声去除可能更复杂，需要根据具体问题进行调整。噪声的性质、小波基函数的选择以及阈值的确定都会影响去噪的效果。

下面再用一个具体示例来演示下处理效果，便于理解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import numpy as np
import matplotlib.pyplot as plt
import pywt

# 生成一个包含噪声的示例信号
np.random.seed(0)
t = np.linspace(0, 1, 1000, endpoint=False)
signal_clean = np.sin(2 * np.pi * 5 * t)  # 原始信号
noise = np.random.normal(0, 0.5, 1000)  # 噪声
signal_noisy = signal_clean + noise  # 含噪声的信号

# 绘制原始信号和含噪声的信号
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.title("Original Signal")
plt.plot(t, signal_clean)

plt.subplot(2, 1, 2)
plt.title("Noisy Signal")
plt.plot(t, signal_noisy)
plt.tight_layout()
plt.show()

# 进行小波变换
wavelet = 'db4'  # 选择小波基函数
coeffs = pywt.wavedec(signal_noisy, wavelet, level=4)

# 设置阈值来去噪
threshold = 0.2  # 根据实际情况调整阈值

def thresholding(x, threshold):
    return pywt.threshold(x, threshold, mode='soft')

coeffs_denoised = [thresholding(coeff, threshold) if i > 0 else coeff for i, coeff in enumerate(coeffs)]

# 重构去噪后的信号
signal_denoised = pywt.waverec(coeffs_denoised, wavelet)

# 绘制去噪后的信号
plt.figure(figsize=(10, 4))
plt.title("Denoised Signal")
plt.plot(t, signal_denoised)
plt.show()

输出：

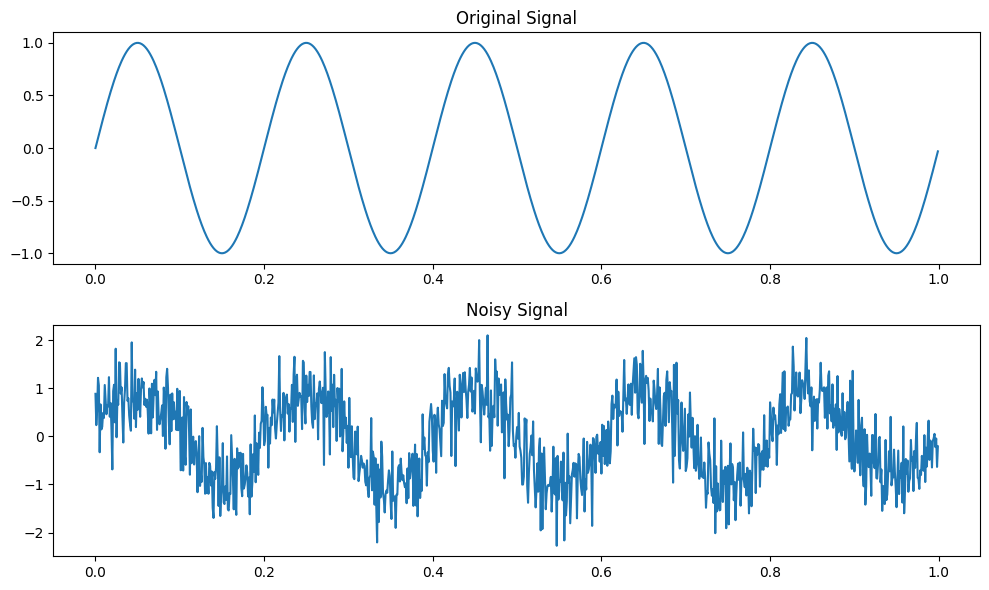
原始信号和加噪信号

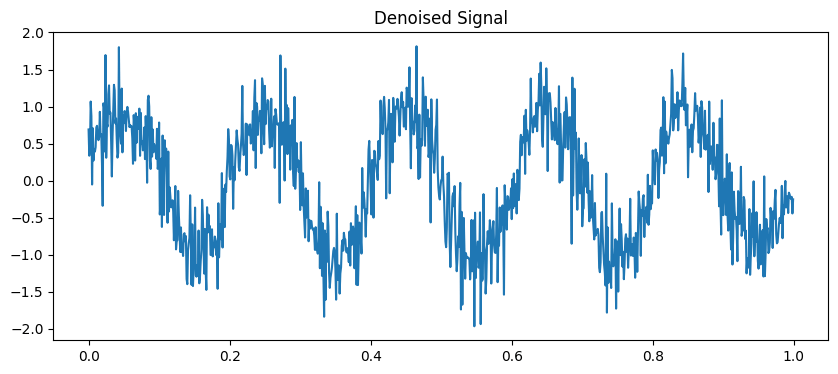
threshold = 0.2

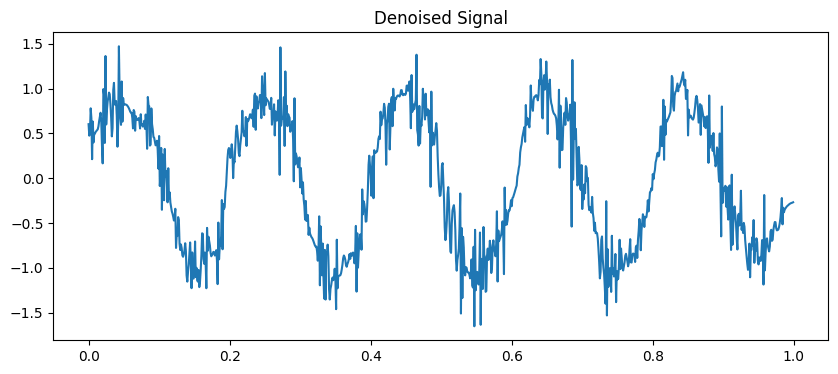
threshold = 0.5

小波变换是一种强大的信号分析工具，可用于在不同尺度和频率上分析信号的特征。