信号去噪之卡尔曼滤波

在前面的文章 卡尔曼滤波 中曾讲解过卡尔曼滤波在惯性导航和飞行姿态控制中的应用，今天来聊一聊卡尔曼滤波在信号去噪中的应用。

卡尔曼滤波（Kalman Filtering）是一种用于估计系统状态的数学方法，它通过考虑系统的动态模型和传感器测量，以最优的方式来融合信息，从而提供对系统状态的最优估计。卡尔曼滤波广泛应用于控制系统、导航系统、信号处理、机器人技术、金融领域等各种领域。

以下是卡尔曼滤波的一些关键要点：

1. 状态空间模型： 卡尔曼滤波将系统建模为一个状态空间模型，其中包括状态变量、状态转移方程和观测方程。状态变量表示系统的内部状态，状态转移方程描述系统如何从一个时刻的状态到下一个时刻的状态演变，观测方程描述了如何从系统状态中获取观测数据。

2. 递归滤波： 卡尔曼滤波是递归的，意味着它在每个时间步骤上都会更新状态估计，同时考虑当前的观测数据和先前的状态估计。

3. 估计与预测： 在每个时间步骤上，卡尔曼滤波执行两个主要步骤：预测和更新。预测步骤使用状态转移方程来估计下一个时刻的状态，而更新步骤使用观测数据来校正预测，并生成最优的状态估计。

4. 协方差矩阵： 卡尔曼滤波通过协方差矩阵来表示状态估计的不确定性。协方差矩阵包含了关于状态估计的信息，可以告诉我们状态估计的精确性和可信度。

5. 最小均方误差： 卡尔曼滤波的目标是最小化状态估计的均方误差，从而提供对系统状态的最优估计。

卡尔曼滤波是一种用于估计具有噪声的动态系统状态的优秀方法。虽然它通常用于估计物理系统的状态，但也可以应用于信号处理和信号去噪中。以下是卡尔曼滤波在信号去噪中的应用示例：

信号模型

首先，我们需要将信号建模为一个状态空间模型，其中状态（信号的真实值）会受到噪声的影响。通常，我们可以将信号建模为一个一维状态空间模型，如下所示：

• 状态（State）：信号的真实值，我们希望估计的值。
• 观测（Measurement）：由于噪声，我们观察到的信号值。
• 过程噪声（Process Noise）：表示信号的状态如何随时间变化的噪声。
• 观测噪声（Measurement Noise）：表示观测信号时的噪声。

卡尔曼滤波算法

卡尔曼滤波通过不断地融合状态估计和观测来提供对信号的估计。以下是卡尔曼滤波的主要步骤：

1. 初始化：初始化状态估计和协方差矩阵。
2. 预测：使用模型预测状态的下一个值，并更新状态估计的协方差矩阵。
3. 观测更新：将观测与预测进行比较，以校正状态估计和协方差矩阵。
4. 重复：重复步骤2和3，以不断更新状态估计和协方差矩阵。

在信号去噪中的应用

在信号去噪中，我们可以将观测值看作是含有噪声的信号，状态估计值则是我们希望获得的干净信号。卡尔曼滤波可以通过融合观测信号和状态预测来估计干净信号。

以下是一个简单的示例，演示了如何在信号去噪中使用一维卡尔曼滤波：

import numpy as np
import matplotlib.pyplot as plt

# 生成一个包含噪声的示例信号
np.random.seed(0)
t = np.linspace(0, 1, 1000)
signal_clean = np.sin(2 * np.pi * 5 * t)  # 原始信号
noise = np.random.normal(0, 0.5, 1000)  # 噪声
signal_noisy = signal_clean + noise  # 含噪声的信号

# 初始化卡尔曼滤波器参数
initial_state = signal_noisy[0]  # 初始状态估计
initial_estimate_error = 1.0  # 初始状态估计误差的方差
process_noise = 0.1  # 过程噪声方差
measurement_noise = 0.5  # 观测噪声方差

# 初始化状态估计和协方差矩阵
state_estimate = initial_state
estimate_error = initial_estimate_error

# 存储估计的信号
estimated_signal = []

# 使用卡尔曼滤波进行信号去噪
for measurement in signal_noisy:
    # 预测步骤
    state_predict = state_estimate
    estimate_error_predict = estimate_error + process_noise

    # 观测更新步骤
    kalman_gain = estimate_error_predict / (estimate_error_predict + measurement_noise)
    state_estimate = state_predict + kalman_gain * (measurement - state_predict)
    estimate_error = (1 - kalman_gain) * estimate_error_predict

    estimated_signal.append(state_estimate)

# 绘制原始信号、含噪声的信号和估计的信号
plt.figure(figsize=(12, 6))
plt.plot(t, signal_clean, label="Original Signal")
plt.plot(t, signal_noisy, label="Noisy Signal")
plt.plot(t, estimated_signal, label="Estimated Signal (Kalman Filter)")
plt.legend()
plt.title("Signal Denoising with Kalman Filter")
plt.show()

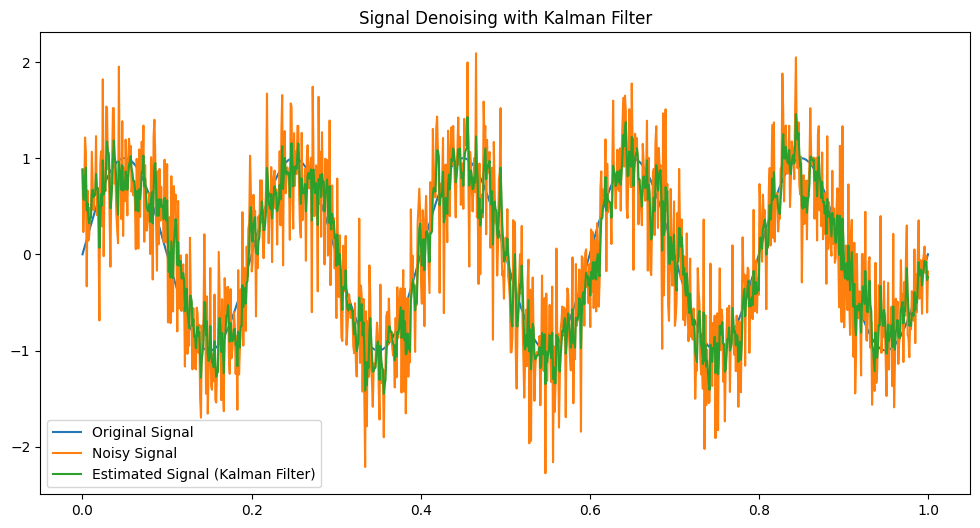
将原始信号与滤波后的信号分开：

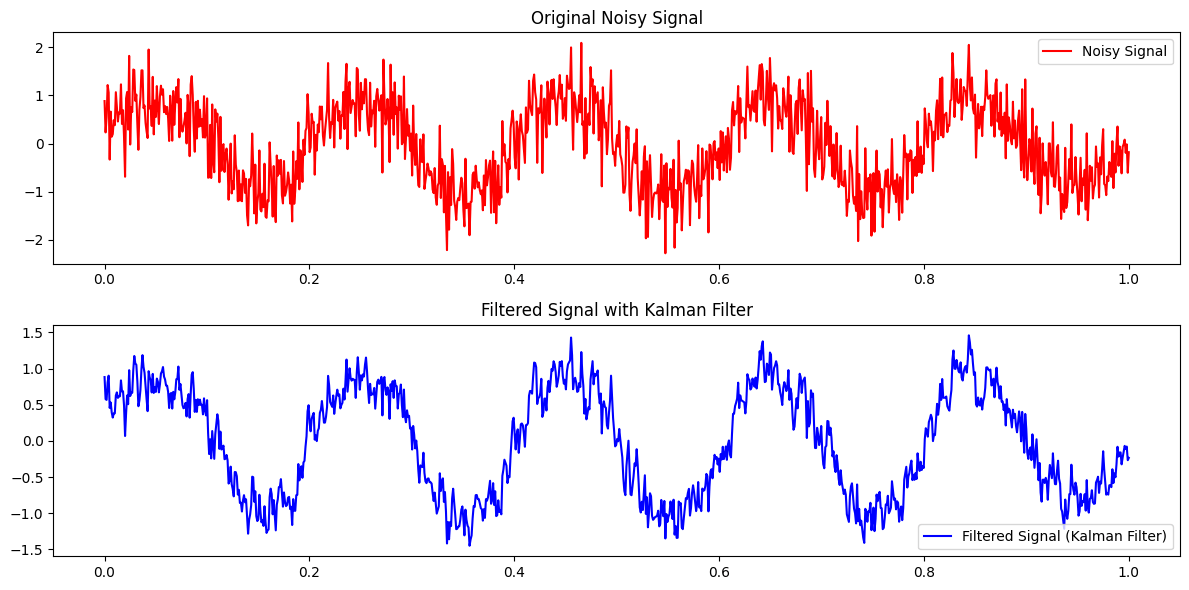
在这个示例中，卡尔曼滤波器通过预测和观测更新逐步估计干净信号。估计的信号（使用卡尔曼滤波）与原始信号进行了比较，以展示去噪效果。卡尔曼滤波的参数需要根据特定的应用和信号特性进行调整。

卡尔曼滤波的主要优点包括对噪声和不确定性的有效处理，以及对系统动态变化的适应能力。然而，它也有一些限制，例如对模型的准确性要求较高，以及对系统和测量噪声的统计性质的要求。