信号去噪

发表于 更新于 阅读次数： 本文字数： 2.6k 阅读时长 ≈ 10 分钟

引言

在实际世界中，我们所获得的信号通常都包含了各种干扰和噪音。这些噪音可能来自电子设备、环境条件或传感器本身，它们会损害信号的质量，降低信息提取的准确性。因此，信号去噪和降噪技术在科学、工程和医学领域中扮演着至关重要的角色。本文将介绍信号去噪的概念、方法和应用。

信号去噪的概念

信号去噪是指从受到噪音干扰的信号中提取出目标信号的过程。目标信号包含我们真正关心的信息，而噪音则包括不相关的、干扰性的信号。信号去噪的目标是尽可能地减少或消除噪音，以恢复原始信号的清晰度。

信号去噪的应用

信号去噪广泛应用于各个领域：

  1. 医学领域：在脑电图（EEG）和心电图（ECG）等生物医学信号中去除肌肉运动和电极噪音，以诊断疾病。

  2. 通信领域：在无线通信中，去除传输过程中的噪音，提高通信质量。

  3. 地球科学：去除地震信号中的地壳噪音，以便检测地震。

  4. 图像处理：在数字图像中降噪以提高图像质量，例如在医学成像中。

  5. 音频处理：去除录音中的杂音，以改善音频质量。

信号去噪方法

信号去噪有多种方法，每种方法都适用于不同类型的信号和噪音。以下是一些常见的信号去噪方法：

  1. 均值滤波：计算信号的移动平均值，以减少随机噪音。

  2. 中值滤波：用信号窗口中的中值替换每个采样点的值，适用于椒盐噪音。

  3. 小波变换：将信号分解成不同尺度的小波系数，通过去除高频小波系数来降低噪音。

  4. 卡尔曼滤波：用于估计具有动态特性的信号中的状态，同时估计噪音。

  5. **独立成分分析 (ICA)**：用于将信号分解成独立的成分，从中识别出目标信号。

  6. 深度学习：使用卷积神经网络（CNN）和循环神经网络（RNN）等深度学习技术，自动学习信号的特征并去除噪音。

  7. **奇异值分解 (SVD)**：将信号矩阵分解成三个矩阵，通过保留主成分降低噪音。

信号去噪的挑战

尽管信号去噪技术取得了巨大进展，但仍然存在一些挑战：

  1. 信号与噪音的分离：在某些情况下，信号和噪音可能在时间或频率上重叠，使得它们难以分离。

  2. 信息丢失：一些去噪方法可能导致有用信息的丢失，因此需要在去噪和信息保留之间做出权衡。

  3. 计算复杂性：某些高级的信号去噪方法需要大量计算资源，这在实时应用中可能是一个挑战。

信号去噪是科学、工程和医学领域中不可或缺的技术之一。通过适当选择和应用信号去噪方法，我们可以提取出清晰的信息，从而做出更准确的决策和发现隐藏在噪音背后的宝藏。

均值滤波

均值滤波（Mean Filtering）是一种基本的信号处理和图像处理技术，用于降低图像或信号中的噪音。它的核心思想是用一定范围内像素或样本的均值来替代每个像素或样本的值，以减少随机噪音的影响。均值滤波在平滑图像、去除图像中的噪声或用于数据预处理等许多应用中都有广泛的应用。

下面详细讲解均值滤波的原理、步骤和应用：

原理

均值滤波的原理非常简单，它基于以下思想：在一个图像或信号中，噪音通常是随机的，因此噪音的均值在一个局部区域内接近于零。相反，信号的均值在同一区域内应该比较稳定。因此，通过在一个局部窗口内计算像素或样本的均值，可以用这个均值替代中心像素或样本的值，从而降低噪音的影响。

步骤

均值滤波的步骤如下：

  1. 选择滤波窗口大小：首先，需要选择一个滤波窗口的大小，通常是一个正方形或矩形区域。这个窗口的大小决定了滤波的程度。较大的窗口可以降低更多的噪音，但可能会导致图像或信号的细节丢失。

  2. 在窗口内计算均值：将窗口放置在图像或信号上，以窗口内的像素或样本计算均值。

  3. 用均值替代中心像素或样本的值：将计算得到的均值替代窗口的中心像素或样本的值。这个操作会将噪音减小，同时保留信号的主要特征。

  4. 在整个图像或信号上重复：将上述操作在整个图像或信号上重复进行，直到所有像素或样本都被处理。

应用

均值滤波的应用非常广泛，包括但不限于以下领域：

  1. 图像处理：在数字图像处理中，均值滤波用于平滑图像、去除图像中的椒盐噪声、降低图像的锯齿状边缘等。

  2. 音频处理：在音频信号处理中，均值滤波可用于去除录音中的背景噪音，提高音频质量。

  3. 数据分析：在时间序列数据分析中，均值滤波可以用于平滑数据、减小季节性或周期性噪音。

  4. 遥感图像处理：在遥感图像处理中，均值滤波有助于去除图像中的云层或大气干扰。

注意事项：

尽管均值滤波是一种简单且易于理解的滤波方法，但它也有一些局限性。例如，均值滤波不适用于处理存在脉冲噪音（如椒盐噪音）的情况，因为它只是简单地计算均值，而不考虑噪音的类型。此外，均值滤波可能会导致图像或信号的模糊化，因此在一些应用中可能不适用，特别是对于需要保留细节的情况。

在实际应用中，人们通常会根据特定问题的要求选择适当的滤波方法，有时也会将均值滤波与其他滤波技术结合使用，以达到更好的去噪效果。

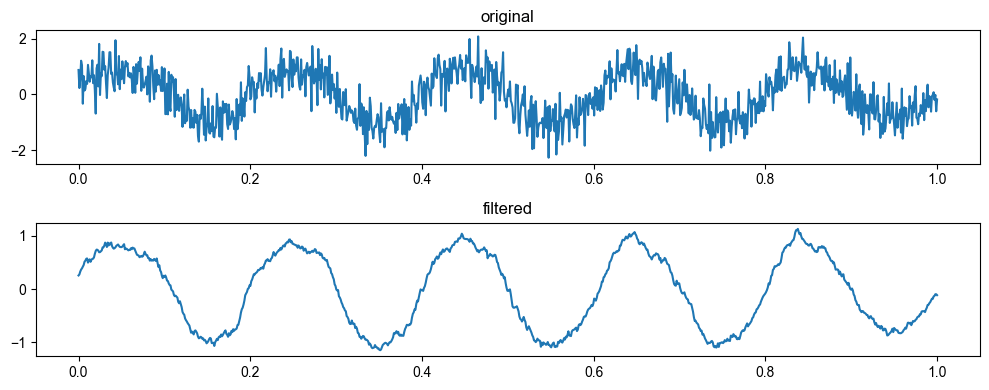
示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
import matplotlib.pyplot as plt


# 生成示例信号，包含高频噪声
np.random.seed(0)
t = np.linspace(0, 1, 1000)
signal = np.sin(2 * np.pi * 5 * t) + 0.5 * np.random.randn(1000)

# 绘制原始信号
plt.figure(figsize=(10, 4))
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.title('original')

# 进行均值滤波去除高频噪声
window_size = 20  # 滤波窗口大小
filtered_signal = np.convolve(signal, np.ones(window_size) / window_size, mode='same')

# 绘制去噪后的信号
plt.subplot(2, 1, 2)
plt.plot(t, filtered_signal)
plt.title('filtered')

plt.tight_layout()
plt.show()

均值滤波去除高频噪声

中值滤波

中值滤波是一种常用的信号处理和图像处理技术，用于去除噪音和平滑信号。与均值滤波不同，中值滤波不是基于平均值，而是使用中间值（即中位数）来代替每个数据点。这种方法对于去除脉冲噪声和椒盐噪声等异常值非常有效，因为中值不受异常值的干扰。

以下是关于中值滤波的详细讲解：

中值滤波的步骤：

  1. 定义一个窗口：首先，您需要定义一个窗口大小，通常是一个正方形或矩形区域，窗口的大小决定了中值滤波器考虑的邻域范围。窗口的大小越大，平滑效果越强，但也可能导致图像细节的丢失。

  2. 将窗口应用到信号：将窗口滑动遍历整个信号。对于每个窗口位置，将窗口内的所有数值按大小排序，并选择中间值（中位数）作为输出值。这个中位数值将替代窗口内的中心数据点的值。

  3. 重复步骤2：继续将窗口移动到信号的下一个位置，然后重复步骤2，直到覆盖整个信号。

中值滤波的优点：

  • 去除噪声：中值滤波对于脉冲噪声、椒盐噪声等异常值非常有效，因为它选择窗口内的中间值，不受极端值的干扰。

  • 保留边缘信息：相对于均值滤波，中值滤波更能够保留图像的边缘信息，因为它不会使边缘变得模糊。

中值滤波的缺点：

  • 不适用于高斯噪声：中值滤波不适用于连续的高斯噪声，因为它不能有效地减少这种类型的噪声。

  • 窗口大小选择：窗口大小的选择对于中值滤波的效果非常重要。选择太小的窗口可能无法有效去除噪声，而选择太大的窗口可能导致图像过度平滑。

示例代码：

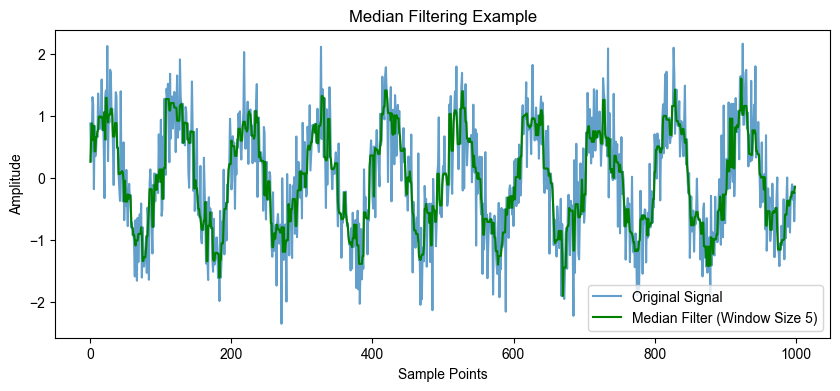
以下是使用Python和NumPy库进行中值滤波的示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
from scipy.signal import medfilt
import matplotlib.pyplot as plt

# Create a sample signal with noise
np.random.seed(0)
signal = np.sin(2 * np.pi * 0.01 * np.arange(0, 1000)) + 0.5 * np.random.randn(1000)

# Apply median filtering
window_size = 5  # Window size
smooth_signal = medfilt(signal, kernel_size=window_size)

# Plot the original and smoothed signals
plt.figure(figsize=(10, 4))
plt.plot(signal, label='Original Signal', alpha=0.7)
plt.plot(smooth_signal, label=f'Median Filter (Window Size {window_size})', color='green')
plt.legend()
plt.title('Median Filtering Example')
plt.xlabel('Sample Points')
plt.ylabel('Amplitude')
plt.show()

中值滤波

将原始信号和滤波后的信号分开绘制：

中值滤波

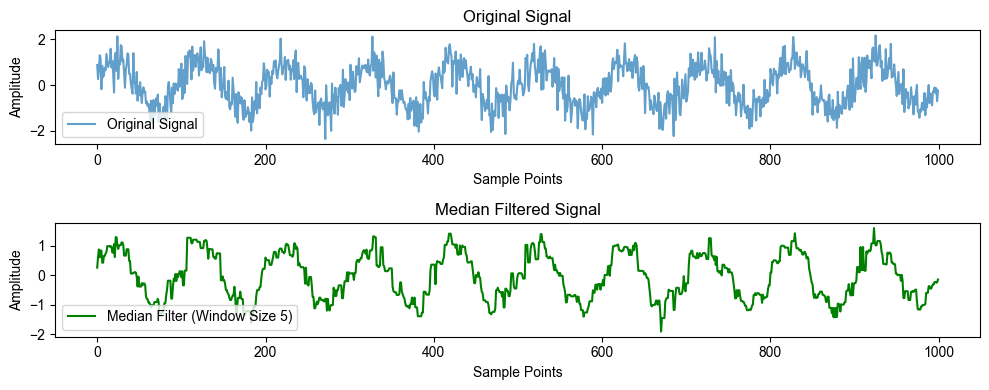
在这个示例中，我们首先创建了一个包含噪声的示例信号，然后使用medfilt函数应用了中值滤波。通过调整window_size，您可以改变窗口的大小，以适应不同类型的噪声和信号。

总的来说，中值滤波是一种强大的去噪工具，特别适用于去除脉冲噪声和椒盐噪声，但需要注意选择适当的窗口大小以平衡去噪和信号保留之间的权衡。