python绘制rc低通滤波器波形图并与spice对比

之前的文章 python绘制rc低通滤波器bode图 中以rc低通滤波器为例，讲解了用python绘制bode图的方法。

本文介绍如何用python绘制波形图，并以rc低通滤波器为例，分别绘制波形图，直观理解滤波器的作用。

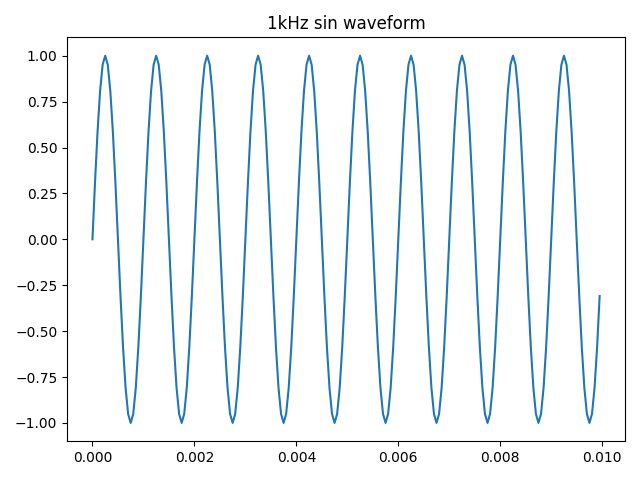
简单正弦波

先绘制一个1kHz的正弦波形：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 设置采样频率
fs = 20000
T = 1/fs

# 生成采样点，时长0.01秒
t = np.arange(0, 0.01, T)

# 生成信号
x1 = np.sin(2*np.pi*1000*t)

# 时域波形
plt.plot(t, x1)
plt.title("1kHz sin waveform")

# 绘制
plt.show

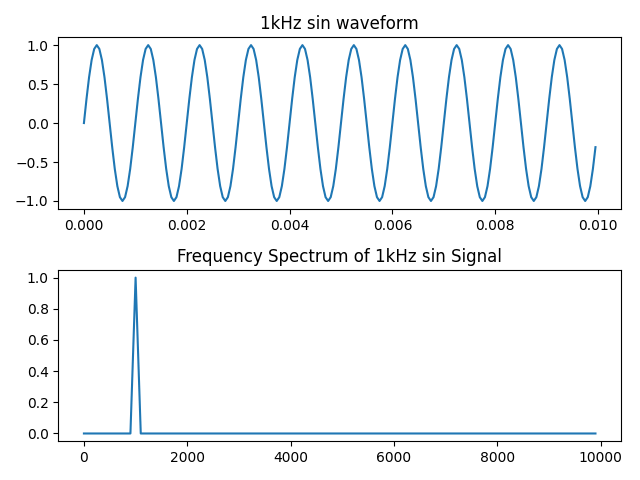
可以把频域图也加进去：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 设置采样频率
fs = 20000
T = 1/fs

# 生成采样点，时长1秒
t = np.arange(0, 0.01, T)

# 生成信号
x1 = np.sin(2*np.pi*1000*t)

# 时域图
plt.subplot(2, 1, 1)
plt.plot(t, x1)
plt.title("1kHz sin waveform")

# 频域图
plt.subplot(2, 1, 2)
f = np.arange(0,fs/2,fs/len(x1))
Y = np.fft.fft(x1)/len(x1)*2
plt.plot(f, abs(Y[:len(Y)//2]))
plt.title('Frequency Spectrum of 1kHz sin Signal')

plt.tight_layout()
plt.show()

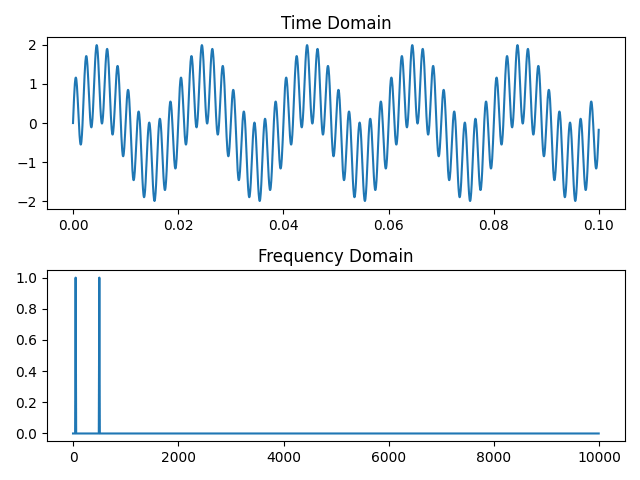
复合波形

下面将1个50Hz正弦波和1个500Hz正弦波复合：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 设置采样频率
fs = 20000
T = 1/fs

# 生成采样点，时长0.1秒
t = np.arange(0, 0.1, T)

# 生成信号
x1 = np.sin(2*np.pi*50*t)
x2 = np.sin(2*np.pi*500*t)
x = x1 + x2

# 时域
plt.subplot(2,1,1)
plt.plot(t, x)
plt.title('Time Domain')

# 频域
plt.subplot(2,1,2)
f = np.arange(0,fs/2,fs/len(x))
Y = np.fft.fft(x)/len(x)*2
plt.plot(f, abs(Y[:len(Y)//2]))
plt.title('Frequency Domain')

plt.tight_layout()
plt.show() 

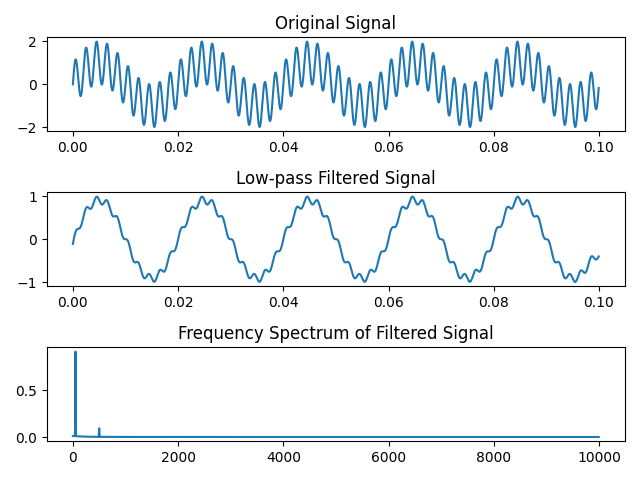
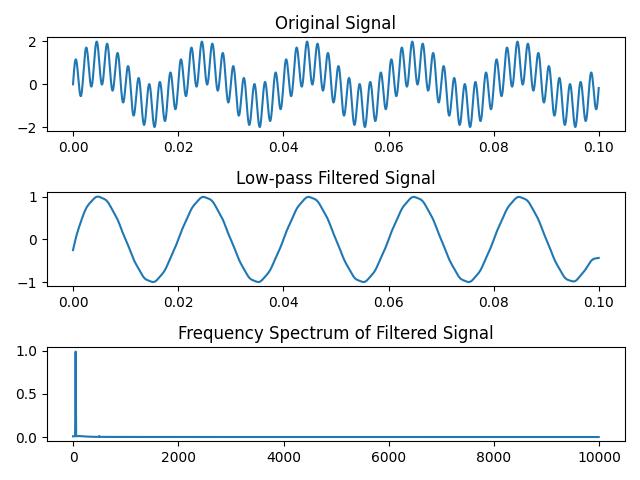
低通滤波器

用python信号库的滤波器对上述复合波形进行滤波：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 设置采样频率
fs = 20000
T = 1/fs

# 生成采样点，时长0.1秒
t = np.arange(0, 0.1, T)

# 生成信号
x1 = np.sin(2*np.pi*50*t)
x2 = np.sin(2*np.pi*500*t)
x = x1 + x2


# 时域绘制原始信号
plt.subplot(3,1,1)
plt.plot(t, x)
plt.title('Original Signal')

# 设计低通滤波器
fc = 159 # 截止频率159Hz
Wn = (fc/(fs/2))
b, a = signal.butter(1, Wn, 'low')

# 应用滤波器
y = signal.filtfilt(b, a, x)

# 时域绘制滤波后的信号
plt.subplot(3,1,2)
plt.plot(t, y)
plt.title('Low-pass Filtered Signal')

# 频域绘制滤波后的信号
plt.subplot(3,1,3)
f = np.arange(0,fs/2,fs/len(y))
Y = np.fft.fft(y)/len(y)*2
plt.plot(f, abs(Y[:len(Y)//2]))
plt.title('Frequency Spectrum of Filtered Signal')

plt.tight_layout()
plt.show()

可以看到1阶低通滤波器将500Hz信号衰减很多，但是依然存在，在不改变截止频率的情况下，我们可以增加滤波器的阶数来达到更好的滤波效果。

2阶滤波器的输出就比较平滑了，已经很接近正弦波形。python信号库中的这个滤波器是数字滤波器，我们可以用它来直观了解滤波器特性，但绘制的波形与实际rc电路会有所区别，要获得更接近实际电路的波形，可以借助spice仿真。

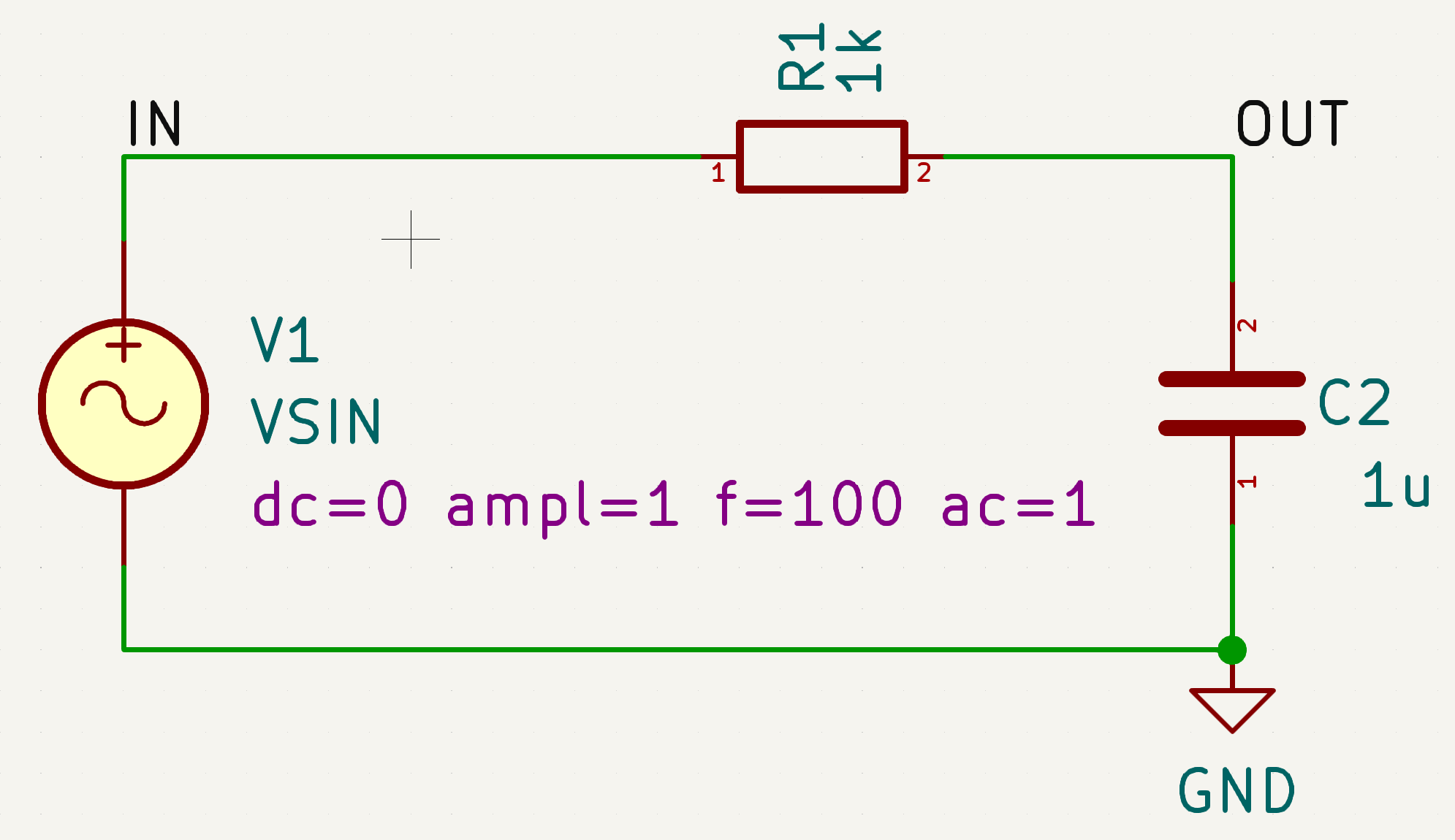
spice仿真

spice有很多衍生版本，这里使用kicad内置的仿真工具进行仿真，它基于ngspice引擎。

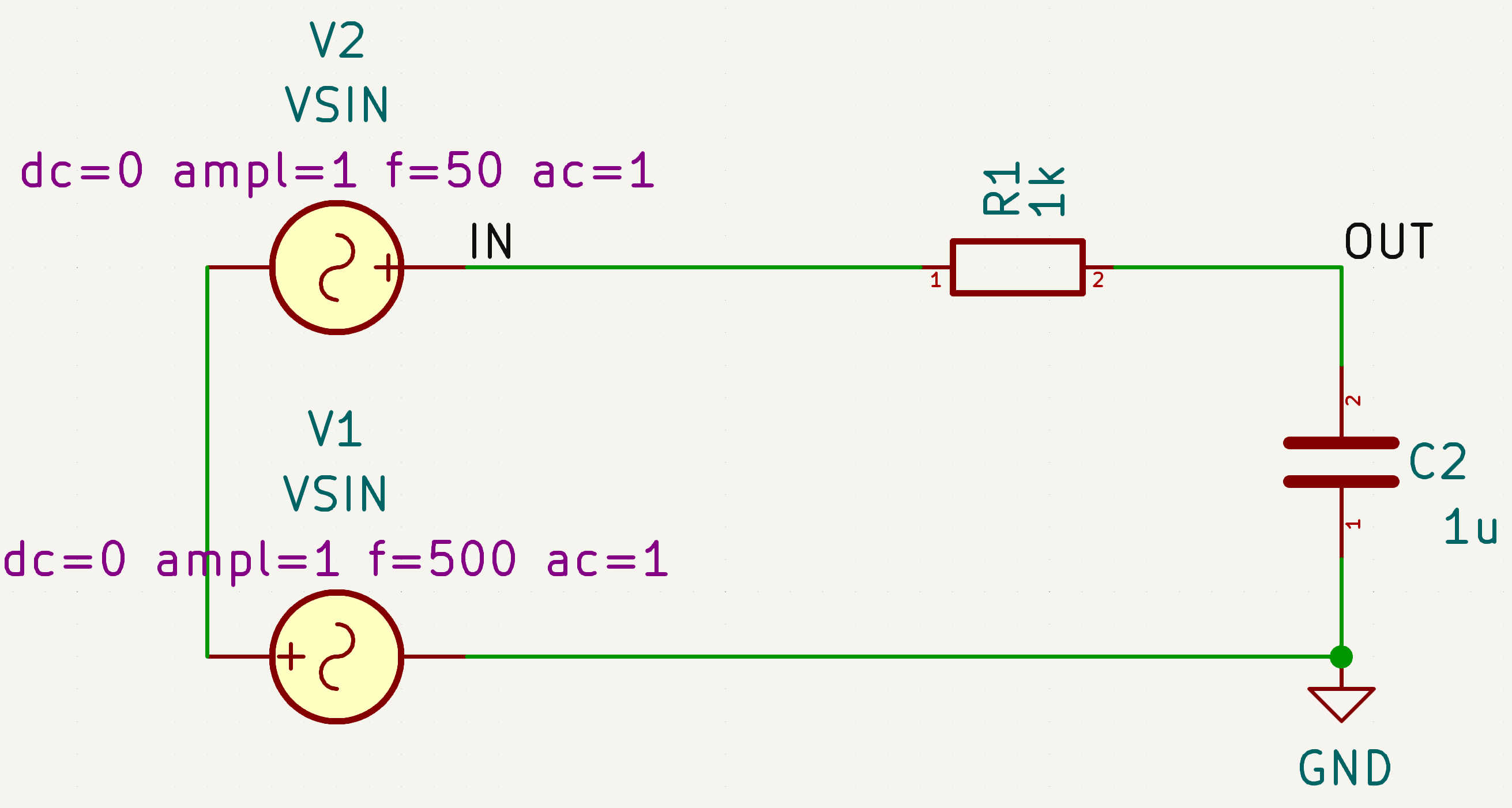
先画原理图：

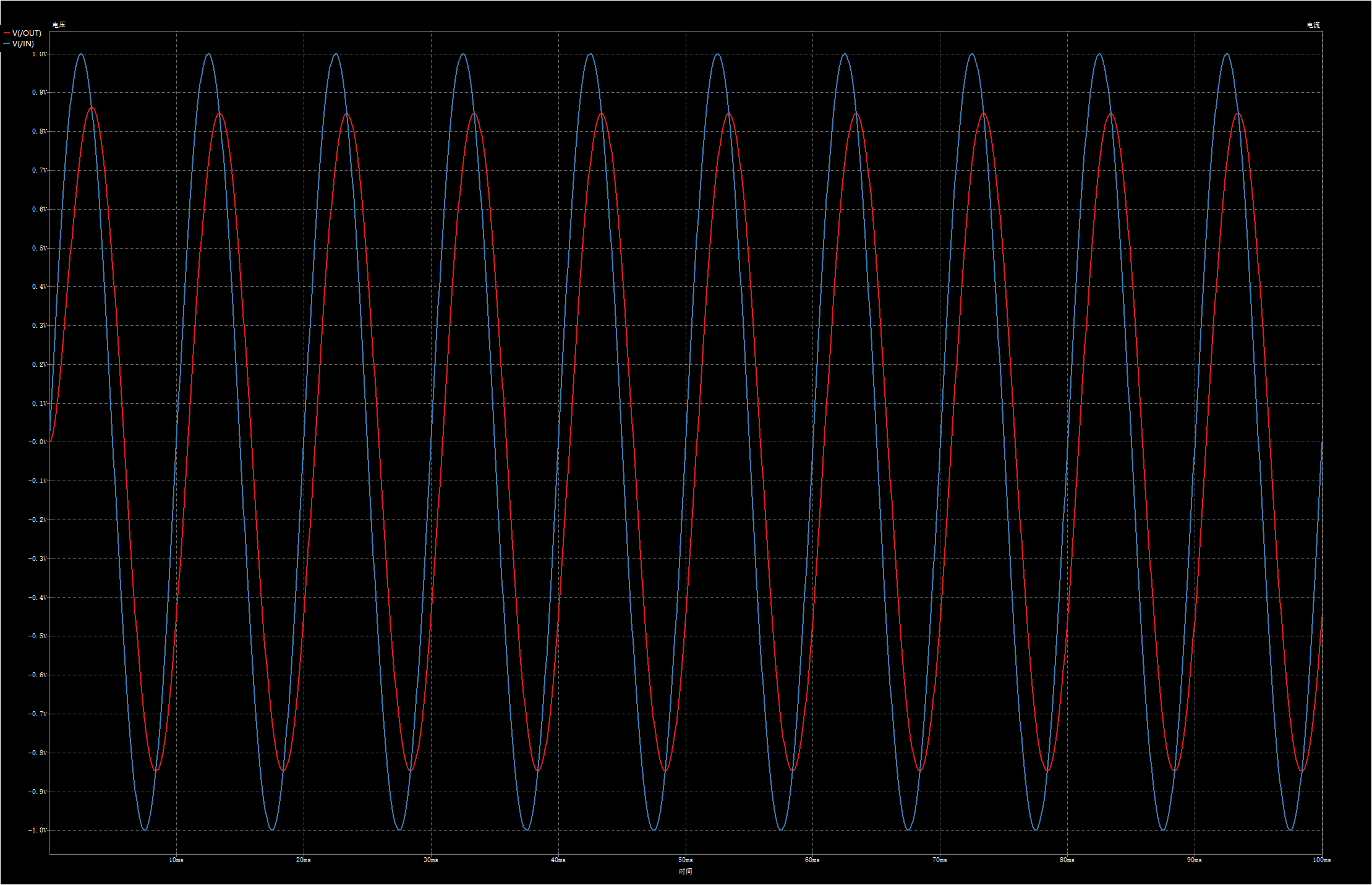
在python绘制rc低通滤波器bode图这篇文章中，我们已经知道1kΩ电阻和1uF串联的1阶RC低通滤波器截止频率是159.15Hz，在上面的原理图中，我设置信号源频率为100Hz，我们先看下仿真输出：

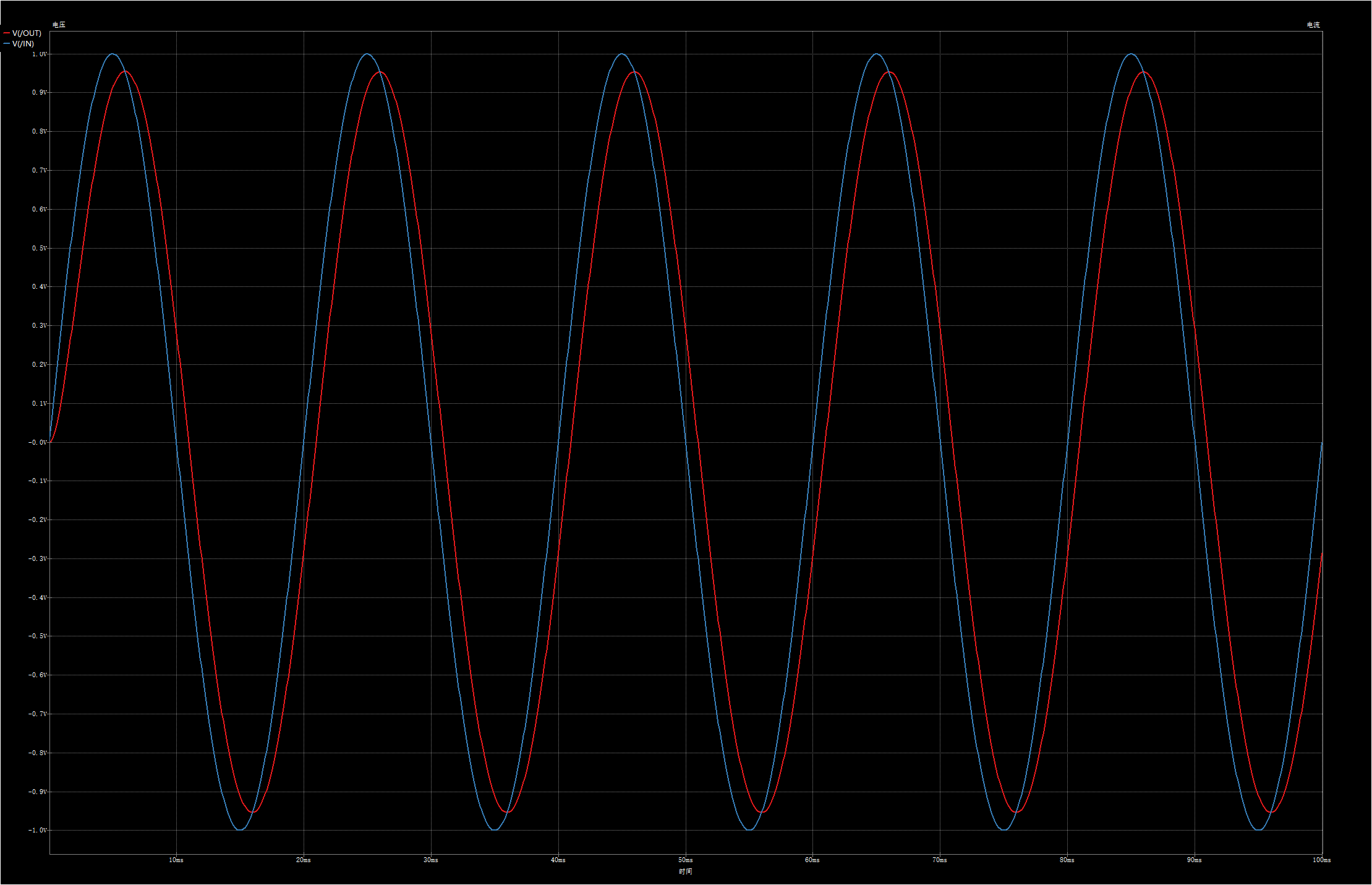
可以看到100Hz的信号已经有所衰减，我们再试一下50Hz的信号：

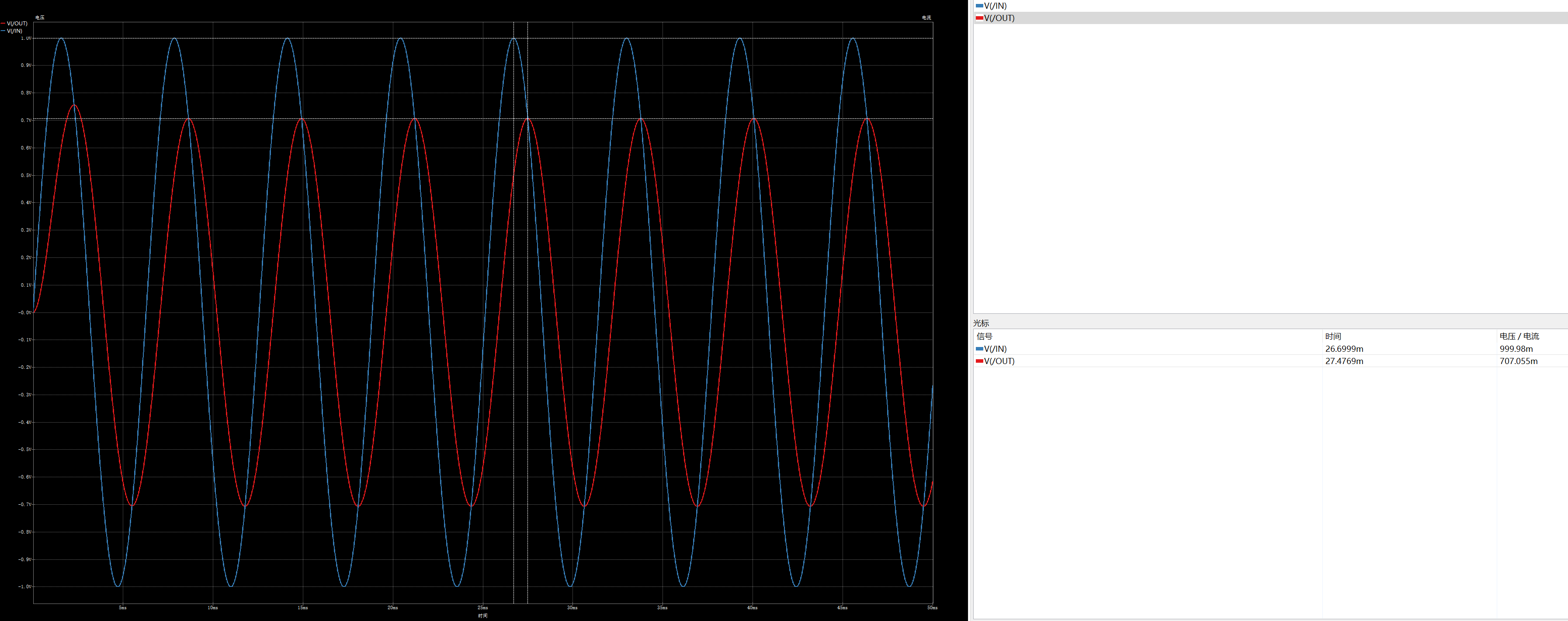
50Hz的信号衰减要小一些。从前面2个仿真波形中，不仅能看到输出信号幅度变化，还能看到相位变化。接下来我们验证下python绘制rc低通滤波器bode图这篇文章中的bode图，设置信号源频率为159.15Hz，看下仿真输出：

理论上，低通滤波器截止频率幅度-3dB，相位-45°。从上面的图中可以看到，输出信号幅度约为707mV，是输入的-3dB，相位需要算一下：

$$
\Delta t = 27.477 - 26.7 = 0.777 ms
$$

45°为1/8周期，对于159.15Hz的信号，45°对应为：

$$
t = \frac {T} {8} = \frac {1} {8f} = \frac {1} {159.15 \times 8} = 0.785 ms
$$

考虑到光标是手动鼠标移动的，仿真结果与理论结果应该可以算是一致的。

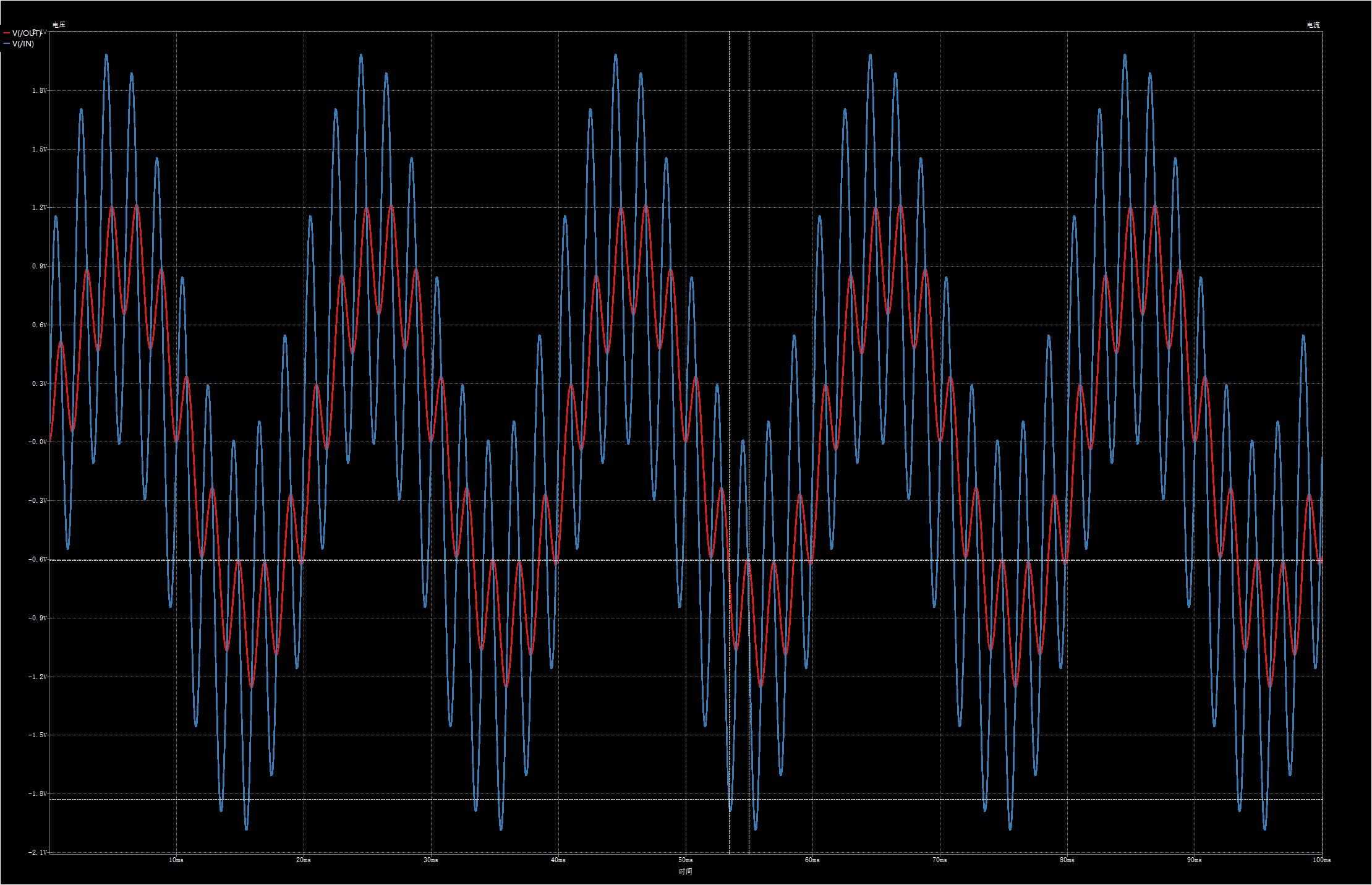
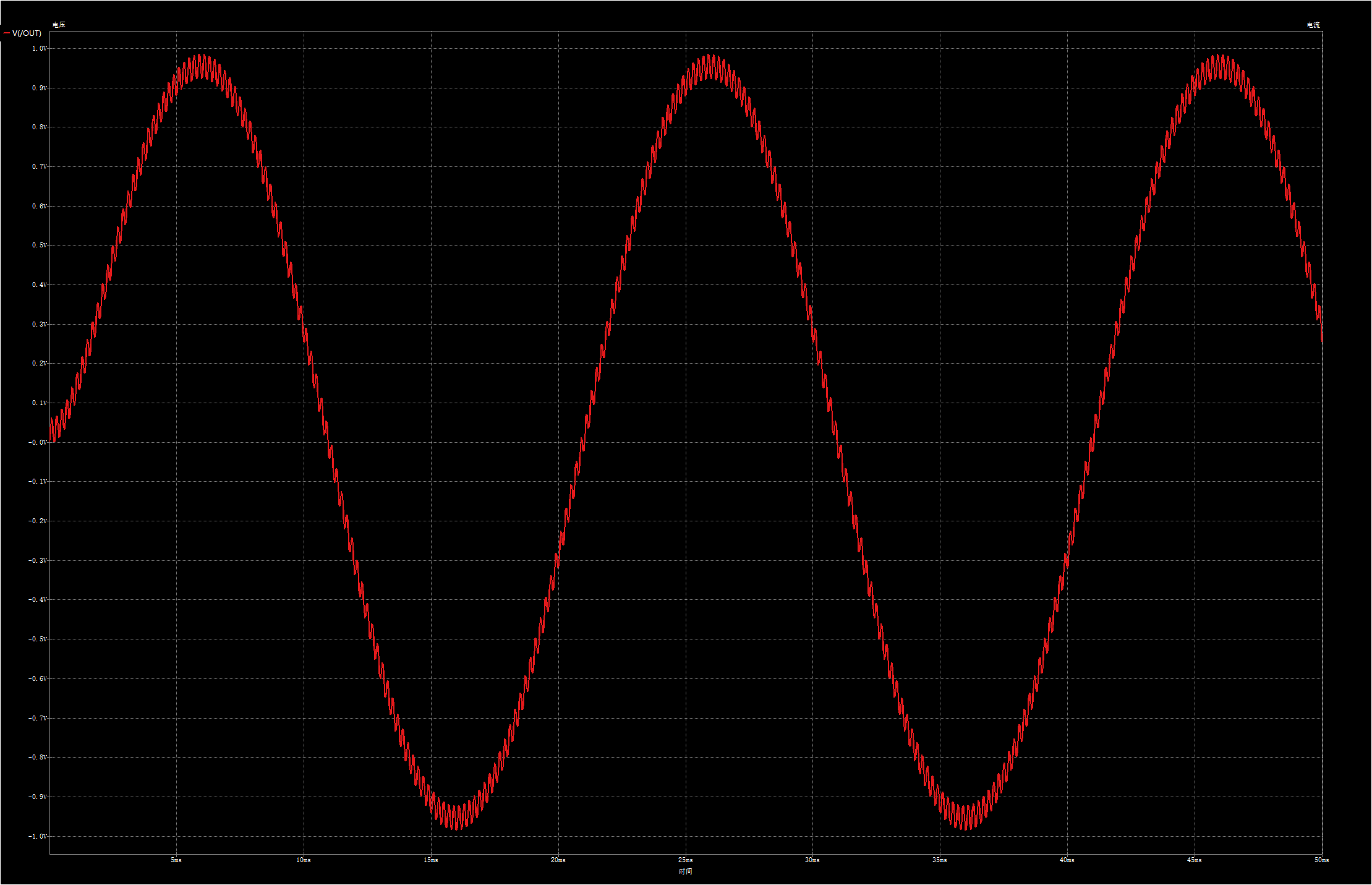
下面我们再来仿真下滤波效果：

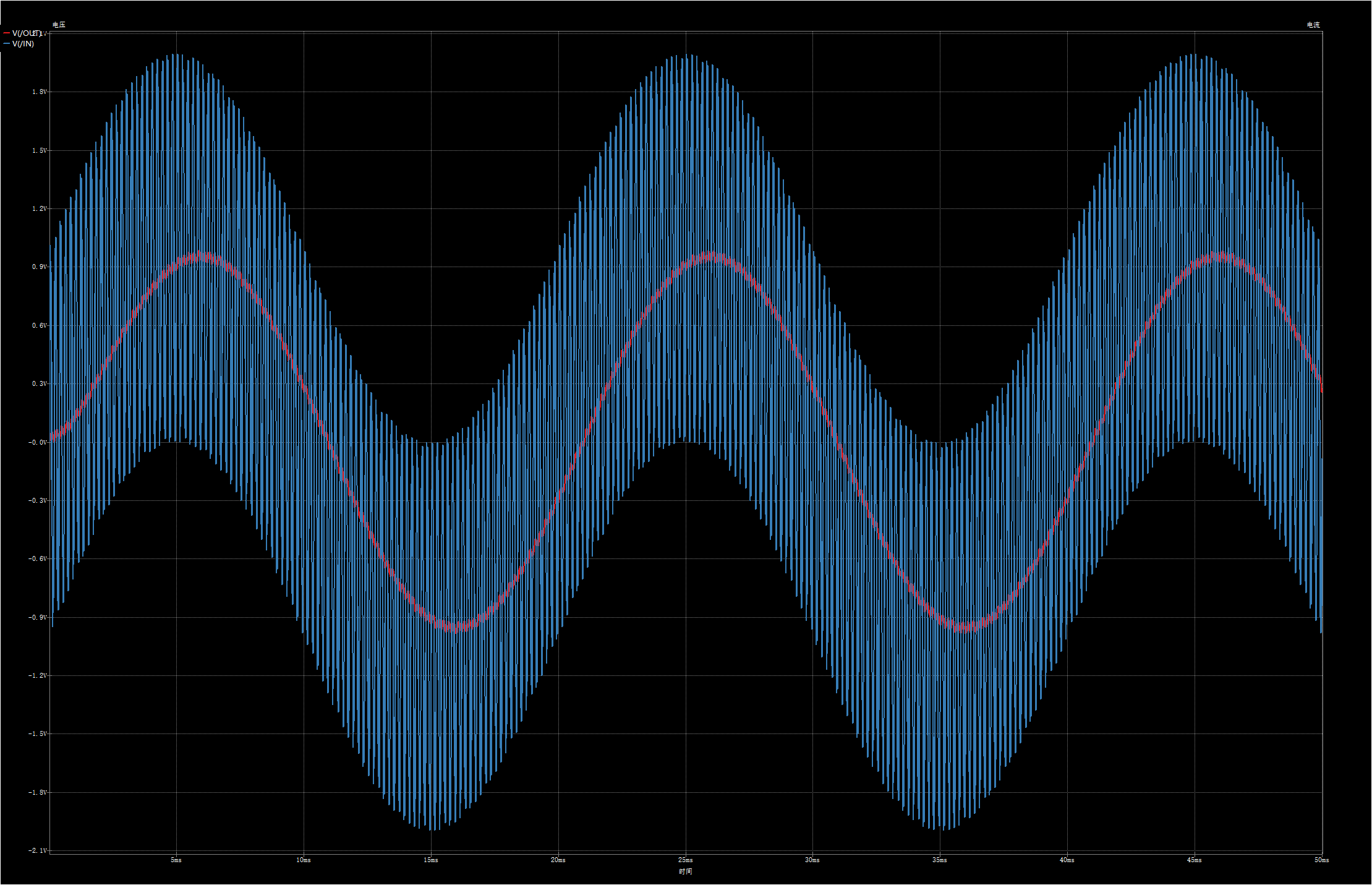
输入信号与上面python代码一致，50Hz和500Hz的正弦波，可以看出滤波效果不太好，1阶rc滤波器滚降速率是10dB/decade，即每10倍频衰减10dB，我们把高频信号从500Hz改为5000Hz再试一下：

可以看到5000Hz的信号已经被衰减到非常小了。