python绘制rc低通滤波器bode图

Bode图

Bode图(国内有译作“伯德图”，也有译作“波特图”)是一种用于描述线性系统的频率响应的图形工具。频率响应是指系统对不同频率的输入信号的响应程度，通常用幅度和相位来表示。Bode图以对数坐标轴的形式显示系统的幅频特性和相频特性，通常使用dB和度作为单位。

Bode图通常由两个子图组成：幅频特性图和相频特性图。幅频特性图显示系统对输入信号的不同频率的响应，横轴为频率，纵轴为幅度，以dB为单位。相频特性图显示系统对输入信号不同频率的相位响应，横轴为频率，纵轴为相位，以度为单位。

在幅频特性图中，Bode图的曲线通常由两个部分组成：低频段和高频段。在低频段，幅度响应随着频率的增加而增加；在高频段，幅度响应随着频率的增加而减小。相位曲线的形状也会随着频率变化而变化。在低频段，相位曲线的斜率比较平缓，而在高频段，相位曲线的斜率比较陡峭。

Bode图可以用来分析系统的稳定性和性能特性。例如，如果系统的幅频特性曲线在截止频率处穿越0dB水平线，那么该系统可能会产生振荡，因为这意味着系统在该频率处的增益为1，可能引起反馈环路不稳定。另外，Bode图还可以用于设计控制系统，例如选择合适的控制器增益和频率补偿网络来满足性能要求。

Bode图是一种非常有用的工具，用于描述线性系统的频率响应特性。它可以帮助工程师更好地理解系统的行为，以便更好地设计和优化控制系统。

RC低通滤波器

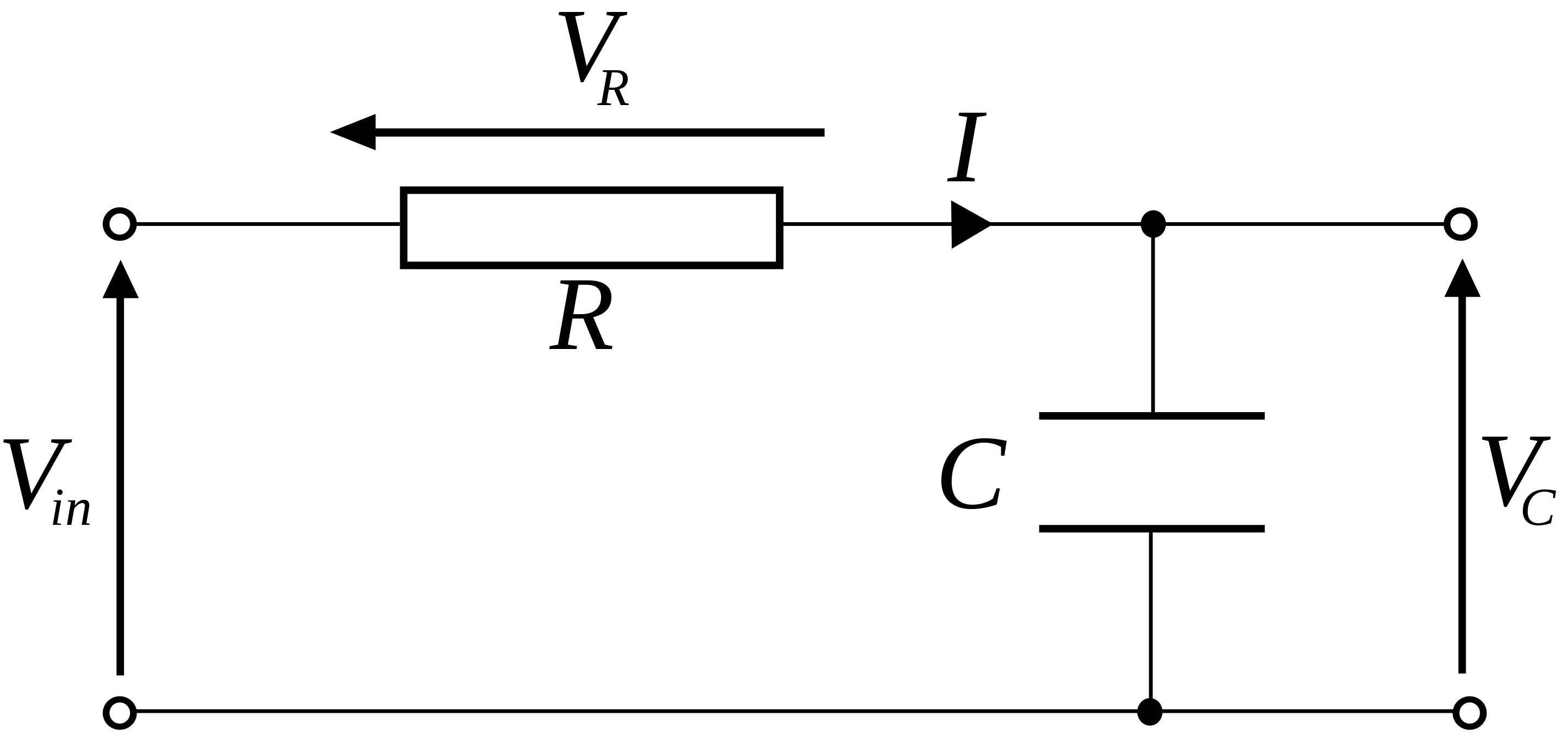
一阶RC滤波器就是电容和电容的串联，电阻和电容对输入信号进行分压，则电容两端电压为：

频域：
$$
\begin{equation}
V_{C}(s) = \frac {1/C_{s}} {R + 1/C_{s}} V_{in}(s) = \frac {1} {1 + RC_{s}} V_{in}(s)
\end{equation}
$$

或时域：
$$
\begin{equation}
V_{C}(t) = V_{in}(t) (1 - e^\frac {-t} {RC})
\end{equation}
$$

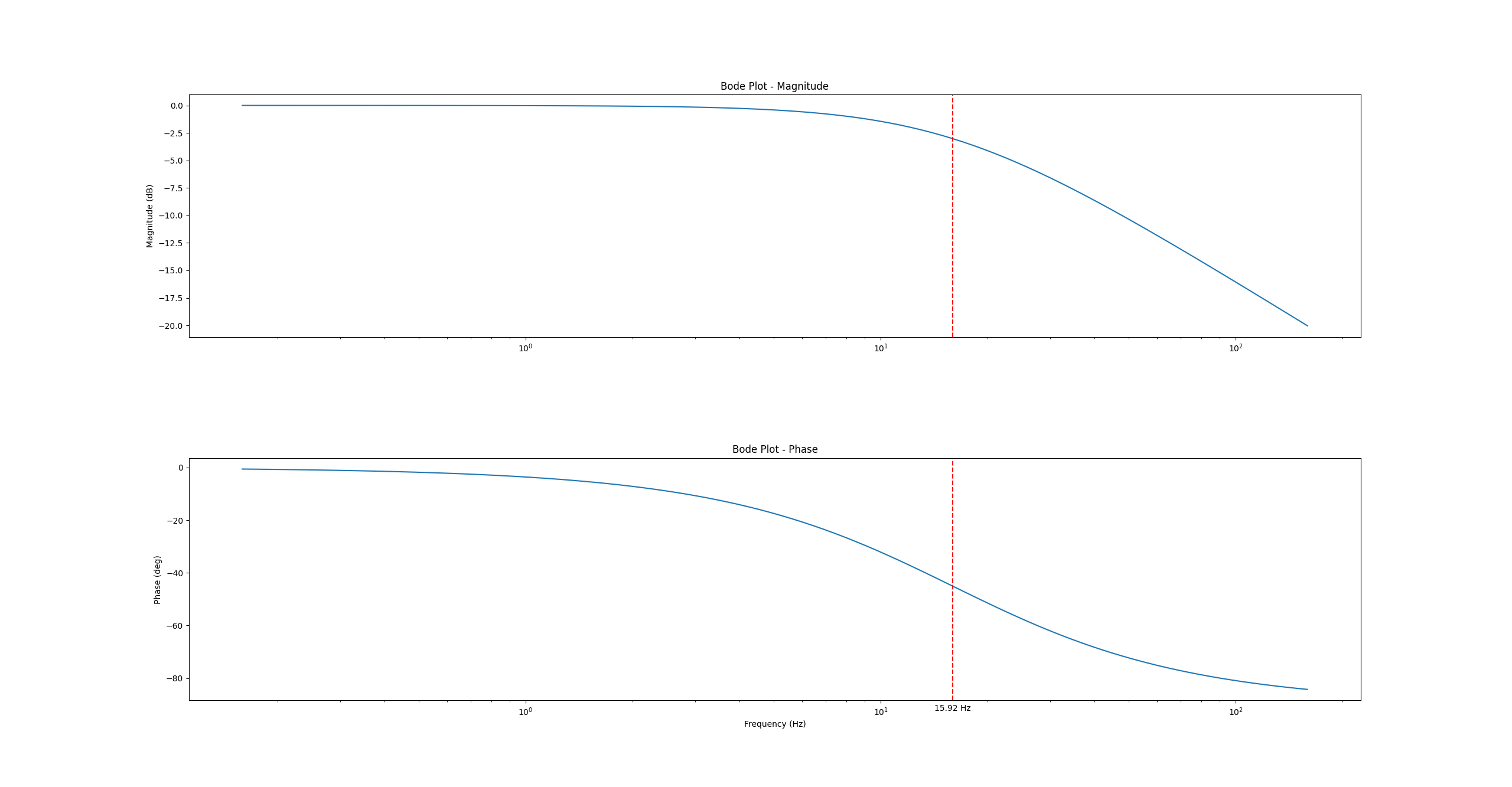
python绘制Bode图

# 导入所需的库：NumPy 用于数学运算，Matplotlib 用于绘图，Scipy 中的 signal 模块用于信号处理。
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 定义 RC 低通滤波器的参数：电阻 R、电容 C 和截止频率 fc。
R = 1000.0   # 电阻值
C = 1e-6     # 电容值
fc = 1 / (2 * np.pi * R * C)  # 截止频率

# 使用 signal.TransferFunction() 函数创建一个一阶 RC 低通滤波器的传输函数 sys，其分子系数为 [1]，分母系数为 [R*C, 1]。
sys = signal.TransferFunction([1], [R*C, 1])
w, mag, phase = signal.bode(sys)

# 创建一个包含两个子图的图形窗口，并返回子图对象 ax1 和 ax2。plt.subplots_adjust() 用于调整子图之间的间距。
fig, (ax1, ax2) = plt.subplots(2, 1)
plt.subplots_adjust(hspace=0.5)

# 在第一个子图中，使用 ax1.semilogx() 绘制幅频响应曲线。ax1.set_title() 和 ax1.set_ylabel() 用于设置子图的标题和 y 轴标签。ax1.axvline() 用于绘制红色虚线，表示截止频率 fc 所在的位置。ax1.text() 用于在截止频率处添加文本标注。
ax1.semilogx(w/(2 * np.pi), mag)
ax1.set_title('Bode Plot - Magnitude')
ax1.set_ylabel('Magnitude (dB)')
ax1.axvline(fc, color='r', linestyle='--')
ax1.text(fc, -40, '{:.2f} Hz'.format(fc), ha='center', va='top')

# 在第二个子图中，使用 ax2.semilogx() 绘制相频响应曲线。ax2.set_title()、ax2.set_xlabel() 和 ax2.set_ylabel() 用于设置子图的标题和轴标签。ax2.axvline() 用于绘制红色虚线，表示截止频率 fc 所在的位置。ax2.text() 用于在截止频率处添加文本标注。
ax2.semilogx(w/(2 * np.pi), phase)
ax2.set_title('Bode Plot - Phase')
ax2.set_xlabel('Frequency (Hz)')
ax2.set_ylabel('Phase (deg)')
ax2.axvline(fc, color='r', linestyle='--')
ax2.text(fc, -90, '{:.2f} Hz'.format(fc), ha='center', va='top')

# 显示图形窗口。
plt.show()

运行结果：

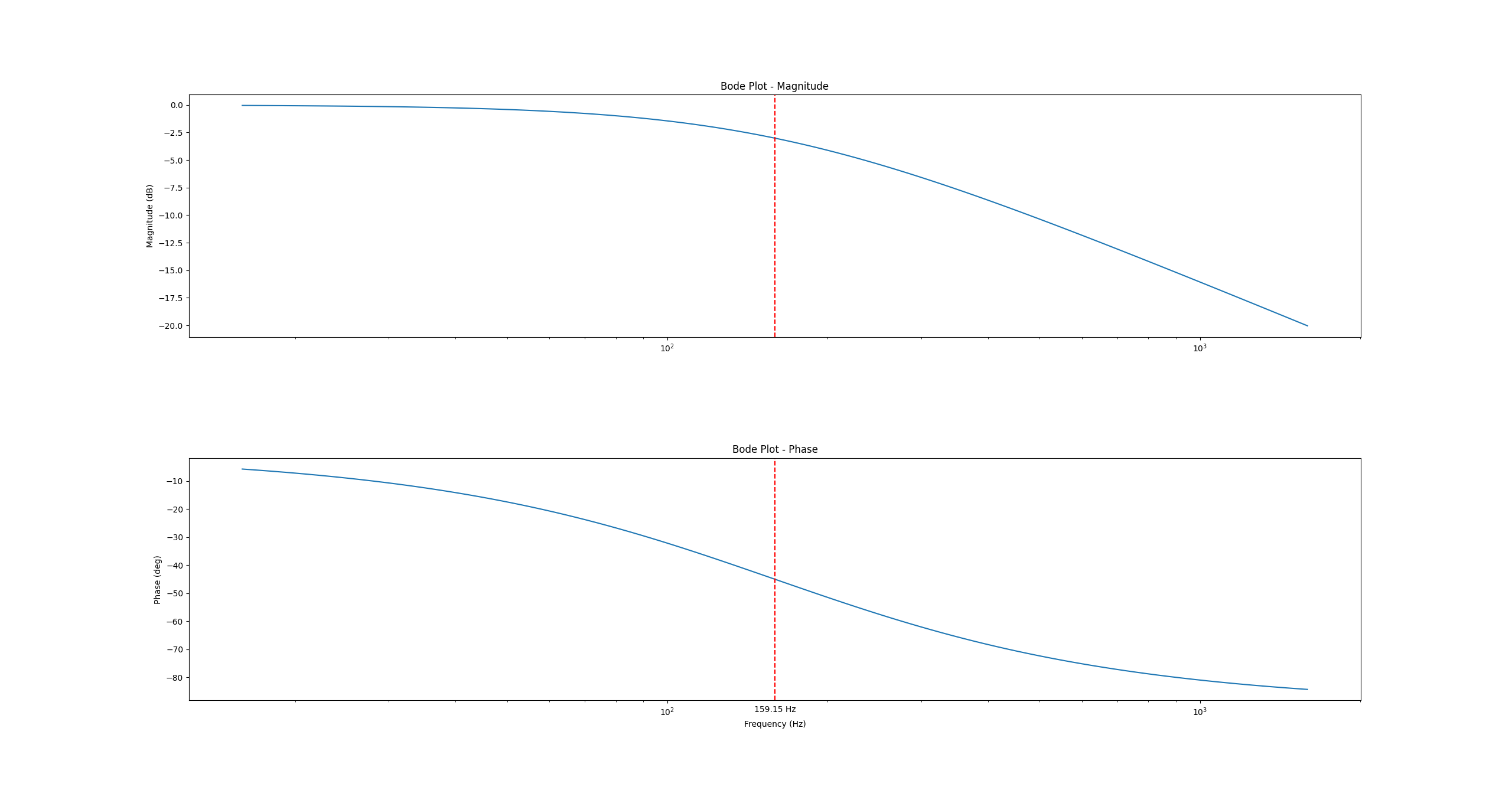
修改一下电阻值，改为10000，再次运行：