信号去噪之独立成分分析（ICA）

发表于 更新于 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 5 分钟

独立成分分析（Independent Component Analysis，ICA）是一种用于从混合信号中分离出原始独立成分的统计方法。它通常用于处理多个传感器捕获的混合信号，旨在找到线性变换，将混合信号转换为独立的源信号，这些源信号在统计上是相互独立的。

以下是关于独立成分分析的一些要点：

  1. 背景和动机： ICA 的应用背景包括语音信号处理、脑电图（EEG）和磁共振成像（fMRI）信号分析、金融数据分析等。在这些情况下，多个信号源混合在一起，我们希望从混合信号中还原原始的信号源，以便进一步分析。

  2. 统计独立性： ICA 的核心概念是统计独立性。在混合信号中，不同的信号源应该在统计上是独立的，这意味着它们的联合概率分布可以分解为各个源信号的概率分布的乘积。

  3. 盲源分离： ICA 被称为“盲源分离”方法，因为它不需要关于信号源的先验信息。它只依赖于混合信号的统计性质来分离信号源。

  4. 混合模型： ICA 假设混合信号可以表示为线性组合的形式，其中每个信号源通过一定的权重系数相加。这可以用矩阵形式表示为 X = AS，其中 X 是混合信号矩阵，A 是混合矩阵，S 是源信号矩阵。

  5. 优化算法： ICA 的目标是找到一个逆变换矩阵 W，使得 Y = WX，其中 Y 是分离后的信号矩阵。这可以通过最大化信号的独立性来实现，通常使用的优化算法包括最大似然估计（MLE）和信息最大化（Infomax）等。

  6. 应用领域： ICA 在许多领域有广泛的应用，包括语音信号分离、脑信号分析、图像分析、信号压缩等。在脑信号分析中，ICA 可用于从脑电图（EEG）或磁共振成像（fMRI）数据中提取潜在的脑区活动。

独立成分分析方法

ICA的目标是找到一种变换，将多个观测信号转换为一组相互独立的信号，这些信号在统计上是不相关的。

具体方法：

1. 问题描述

假设我们有多个观测信号，表示为 $x(t)$，其中 $t$ 表示时间或空间。这些信号是由若干个独立信号源 $s(t)$ 经过线性混合而成的，即：

$$
x(t) = As(t) + n(t)
$$

其中，$x(t)$ 是观测信号，$A$ 是混合矩阵，$s(t)$ 是独立信号源，$n(t)$ 是噪声。

2. 统计独立性假设

ICA 的核心假设是独立信号源 $s(t)$ 在统计上是相互独立的，这意味着它们的联合概率密度函数可以分解为各个信号源的概率密度函数的乘积。这个假设对于很多实际问题是合理的，例如语音信号分离、图像分析等。

3. 求解过程

ICA 的目标是找到一个逆变换矩阵 $W$，使得 $y(t) = Wx(t)$ 中的 $y(t)$ 是独立信号源 $s(t)$ 的估计。求解过程通常包括以下步骤：

  1. 中心化：首先，对观测信号进行中心化，即减去均值，以消除直流分量的影响。

  2. 白化：白化是一种变换，使观测信号的协方差矩阵成为单位矩阵，从而去除信号的相关性。这可以通过特征值分解来实现。

  3. 寻找分离矩阵 $W$：分离矩阵 $W$ 的选择是关键步骤。它的目标是将白化后的观测信号 $y(t)$ 转换为估计的独立信号源 $s(t)$。通常采用最大似然估计（MLE）或信息最大化（Infomax）等方法来找到适当的 $W$。

  4. 分离信号：使用估计的分离矩阵 $W$，可以得到估计的独立信号源 $s(t)$。

4. 非高斯性质

ICA 的成功建立在信号源 $s(t)$ 具有非高斯性质的假设上。这是因为高斯分布的信号在线性混合后仍然服从高斯分布，不容易分离。

5. ICA 应用

ICA 在各种领域有广泛的应用。在语音信号处理中，它可以用于分离不同说话者的声音。在脑信号分析中，它可以用于从脑电图（EEG）或磁共振成像（fMRI）数据中提取潜在的脑区活动。在图像处理中，它可以用于独立分离出图像中的不同成分，如纹理、边缘等。

python示例

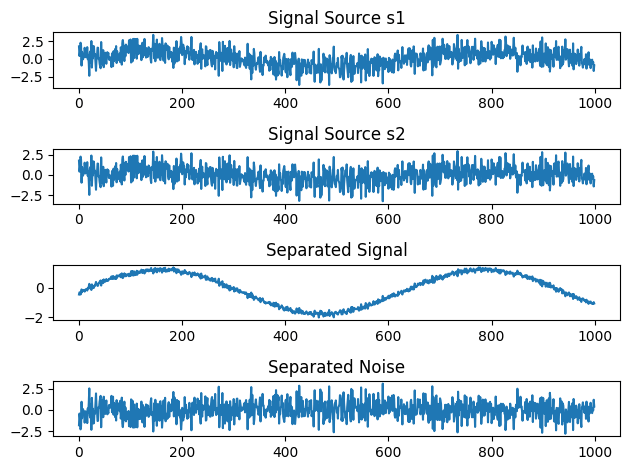
下面是一个基于 Python 和 scikit-learn 库的简单的独立成分分析（ICA）示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
from sklearn.decomposition import FastICA
import matplotlib.pyplot as plt

# 生成混合信号
np.random.seed(0)
time = np.linspace(0, 5, 1000)
signal = np.sin(2 * time)  # 信号源
noise = np.random.normal(size=s1.shape)  # 噪声
s1 = signal + noise
s2 = 0.5 * signal + noise

# 执行独立成分分析
ica = FastICA(n_components=2)
S = np.c_[s1, s2]
S = ica.fit_transform(S)

# 绘制混合信号和分离信号
plt.figure()

plt.subplot(4, 1, 1)
plt.title('Signal Source s1')
plt.plot(s1)

plt.subplot(4, 1, 2)
plt.title('Signal Source s2')
plt.plot(s2)

plt.subplot(4, 1, 3)
plt.title('Separated Signal')
plt.plot(S[:, 0])

plt.subplot(4, 1, 4)
plt.title('Separated Noise')
plt.plot(S[:, 1])

plt.tight_layout()
plt.show()

输出：

ICA分离信号和噪声